Statistical Mechanics
source: wiki
Quantum Mechanical Basis
Only with the advent of quantum mechanics it was possible to delve into the microscopic world of molecules and particles. Without the inclusion of the wave-particle duality in the behaviour of those species, it is not possible to calculate accurate energy spectra nor to understand what really happens at such microscopic scale. It is therefore necessary for us to understand the quantum mechanical basis of molecular physics.
source: wiki
Statistical Mechanical Basis
With the discrete energy spectra of molecules and atoms that we get from quantum mechanics, we can use the statistical mechanical framework to build partition functions and gain access to the thermodynamic properties of large molecular systems. It is by combining these two worlds that we can aim at predicting properties of macroscopic systems using first principles.
Electronic Partition Functions
But in order to go from the properties of one molecule to the properties of a large ensemble of them, we require a specific set of molecular descriptors. Based on the partition we previously did on the energy of a single molecule, the first descriptor we have to consider are electronic energies.
Nuclear Functions
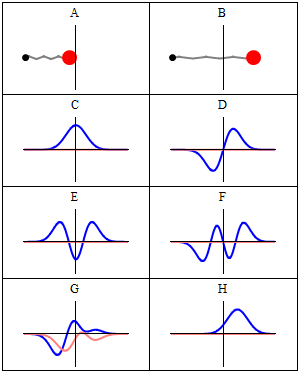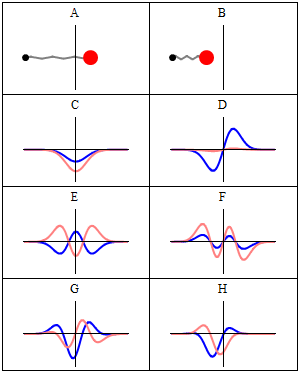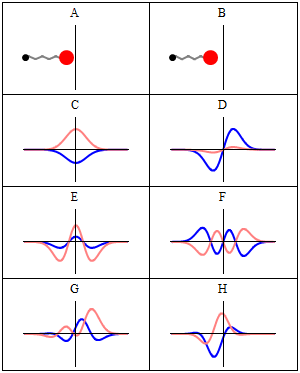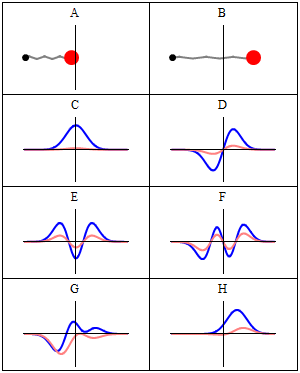
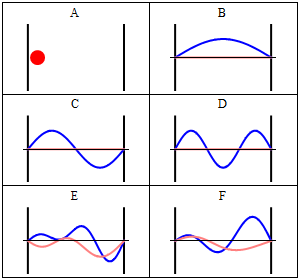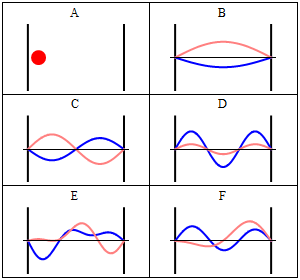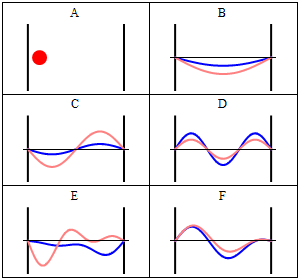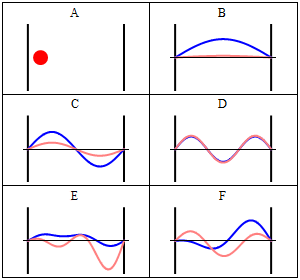
With the electronic contribution to the total energy available we can aim at describing nuclear motion and accounting for it in the partition functions. As mentioned in the first PDF, this includes internal degrees of motion like molecular vibration (for which the simplest model is the harmonic oscillator) and molecular rotation (which typically uses the rigid rotor approximation) as well as the motion of the center of mass (the translation of the particle in a box, for which the simplest model possible is the particle in a box). Finally, there is still the nuclear spin, which is rarely directly accounted in statistical mechanical calculations. This is because in normal conditions nuclear spin states are degenerate, and this contribution to the partition function is just a multiplicative factor.
It is interesting to note that the particle in a box model is the only one that considers the molecules as a whole and does not look into their composition. The energy is thus the same whether the particle is just a point in space and has no structure or whether the particle is a complex protein. Molecular shape and composition is contained in the other three components of the total energy. To the left you have a pictorial descriptions of the quantum harmonic oscillator and of the particle in box model with a representation of some of the solutions to the respective Schroedinger equations.

source: wiki
The Debye Solid
When it comes to the properties of crystals, there are two central models in statistical mechanics. One is the the Einstein crystal, which is developed in most books in on the subject. This model is valid mostly at medium ranged temperatures and requires a phonon frequency that can be estimated by fitting, thus giving access to the thermodynamics of the solid. On the low-temperature range there is the Debye model as well, which requires knowing the density and speed of sound of the crystal. This is the model we develop in the PDF-file below.

source: wiki
Adsorption
The interaction of solids with gases is in itself a very rich subject which finds many scientific and technological applications. The study and understanding of the adsorption of gases to solids is then of great interest in many areas. The framework of statistical mechanics proves itself to be very powerful in explaining these phenomena. Below you have an overview of some topics in adsorption from the perspective of partition functions. Even though most of the statistical mechanical developments are relatively old, I tried grasping a flavour of what is possible to achieve with simulation now-a-days.