Quantum Chemistry
source: wiki
Atoms and Quantum Mechanics
When dealing with molecular physics, it is best to start by giving a solid basis on its foundation. And the foundations of molecules are atoms. The Schroedinger equation for atoms is only analytically solvable for the hydrogen atom or hydrogen like ions, i.e., systems with exactly one electron. Approximations can be used to solve any other atom and the conclusion is that the physical way of describing electrons in any atom is essentially the same.

source: wiki
Molecular Quantum Mechanics
Much like poly-electronic atoms, there is no analytical solution to the molecular Schroedinger equation. To get a (very) good approximation to the molecular wavefunction, one uses the very powerful approximation of linear combination of atomic orbitals. This means that molecular orbitals, the wavefunctions describing electrons in molecules, are built by combining atomic orbitals. There are two main schools of thought in quantum chemistry, one is based on the Hartree-Fock (HF) method while the other is based on density functional theory (DFT). Even though there are recently great advances in Hartree-Fock based methods, there is an obvious dominance of DFT in the world of computational chemistry. This is because considerably good results can be obtained at an amenable computational cost, even though significantly more accurate results can be potentially obtained using post-HF methods.

source: wiki
Atomic Basis Sets
In order to perform molecular calculations, one requires using a set of (precomputed) orbitals describing the atoms. Once again, the world of modern quantum chemistry shows a dominant leader, which are Gaussian Type Orbitals (GTOs) used in most if not all quantum chemistry packages.
However, an alternative type of basis set was never really left outside. These are Slater Type orbitals.
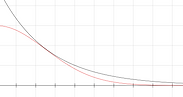
Atomic Basis Sets (cont.)
Neither STOs nor GTOs are correct descriptions of electrons in atoms, these are just approximations. STOs neglect the nodal structure of the hydrogenic orbitals that we mentioned in the first PDF, and GTOs are built to simulate the behaviour of STOs. However, STOs offer a better description at many levels: they are more adequate around the nuclei and they have the proper decay at large electron-nucleus distances. To the left you have a simple plot of an exponential and a Gaussian function and you can see that only at middle range they both decay equivalently. The Gaussian function reaches “0” much faster than the exponential function and the derivatives at x = 0 are completely off.
Though I do not have currently the references for that, typically less STOs are required in order to achieve similar quality in the results of quantum chemical calculations. The problem of STOs is that the calculation of molecular integrals is extremely complicated to say the least. Next I will focus on integral evaluation for STOs. If you are interested in integral evaluation for GTOs I advise you to check libreta and the references therein.

source: wiki
Overlap Integrals
The calculation of the overlap functions is usually done in a local frame where we place both atoms in one of the axis of the referential (typically z). For the overlaps to be consistent with the molecule, it is then essential to rotate the overlaps into the molecular frame.

source: wiki
From Local to Global: the Molecular Frame
The first type of integrals required in quantum chemical calculations are overlap integrals. These measure the overlap between atomic basis functions used in the calculation. Their importance is directly obvious: since we build molecular orbitals from atomic orbitals, it is important to quantify the degree of linear dependency of the basis of atomic orbitals.
source: wiki
Other AO Integrals
As the PDF on HF showed, one also requires kinetic energy integrals and nuclear repulsion integrals. Unfortunately, I was not yet able to find adequate solutions to all nuclear repulsion integrals, and therefore I can only provide for the moment the PDF for the calculation of kinetic energy integrals.
Finally, one also requires electron repulsion integrals (ERIs). More on these soon.
