Nuclear Partition Functions

With the electronic contribution to the total energy available we can aim at describing nuclear motion and accounting for it in the partition functions. As mentioned in the first PDF, this includes internal degrees of motion like molecular vibration (for which the simplest models is the harmonic oscillator approximation) and molecular rotation (which typically uses the rigid rotor approximation) as well as the motion of the center of mass (the translation of the particle in a box, for which the simplest model possible is the particle in a box). Finally, there is still the nuclear spin, which is almost never accounted in statistical mechanical calculations except in very particular cases. This is because in normal conditions nuclear spin states are degenerate, and this contribution to the partition function is just a multiplicative factor.

HarmonicOscillator.pdfDownload

RigidRotor.pdfDownload

ParticleInBox.pdfDownload

NuclearSpin.pdfDownload

It is interesting to note that the particle in a box model is the only one that considers the molecules as a whole and does not look into their composition. The energy is thus the same whether the particle is just a point in space and has no structure or whether the particle is a complex protein. Molecular shape and composition is contained in the other three components of the total energy. Below you have a pictorial description of a particle in box and the respective solutions to the Schroedinger equation (taken from wikipedia). B, C and D represent the first three stationary states of the time-independent Schroedinger equation, whereas E and F are solutions to the time-dependent Schroedinger equation, built as superpositions of stationary states.

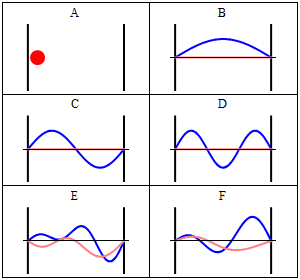
The particle in a box and some wavefunctions, taken from wikipedia (https://upload.wikimedia.org/wikipedia/commons/8/8f/InfiniteSquareWellAnimation.gif)