Atomic Basis Sets

In order to perform molecular calculations, one requires using a set of (precomputed) orbitals describing the atoms. Once again, the world of modern quantum chemistry shows a dominant leader, which are Gaussian Type Orbitals (GTOs) used in most if not all quantum chemistry packages.

GTOs.pdfDownload

However, an alternative type of basis set was never really left outside. These are Slater Type orbitals.

STOs.pdfDownload

SlaterExponents.xlsxDownload

To keep it simple and to be fair, neither STOs nor GTOs are correct descriptions of electrons in atoms, both basis sets are mere approximations. STOs neglect the nodal structure of the hydrogenic orbitals that we mentioned in the first PDF, and GTOs are built to simulate the behaviour of STOs. However, STOs offer a more adequate description at many levels: they are better descriptions of electrons around the nuclei and they have the proper decay at large electron-nucleus distances. Below you have a simple plot of an exponential and a Gaussian function with the same exponent. Despite the shift in x observed between both functions, one can see that at middle range they both decay equivalently. However, the Gaussian function reaches “0” much faster than the exponential function and the derivatives at x = 0 are completely off.

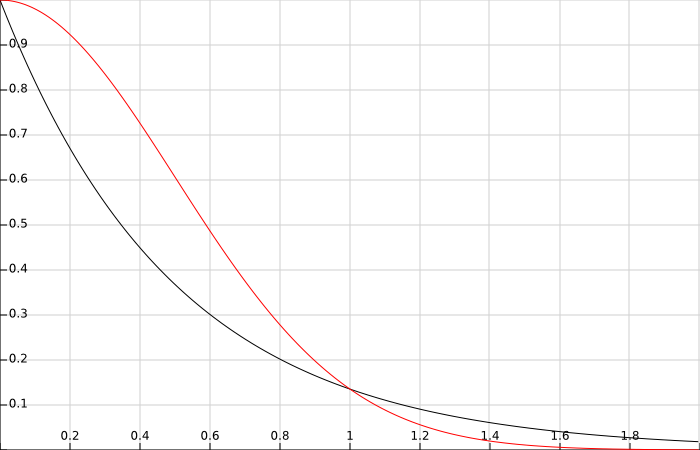
It is therefore observed (though I do not have currently the references for that) that less STOs are required in order to achieve similar quality in the results of quantum chemical calculations. The problem of STOs is that the calculation of molecular integrals is extremely complicated to say the least. In the next paragraphs I will focus only on integral evaluation for STOs. If you are interested in integral evaluation for GTOs I would advice you to check libreta and the references therein (http://www.zhjun-sci.com/software-libreta-download.php).